improving deep neural networks hyperparameter tuning regularization and optimization week 2 quiz answers
Quiz - Optimization Algorithms
1. Which notation would you use to denote the 3rd layer’s activations when the input is the 7th example from the 8th minibatch?
2. Suppose you don't face any memory-related problems. Which of the following make more use of vectorization.
- Batch Gradient Descent
- Stochastic Gradient Descent, Batch Gradient Descent, and Mini-Batch Gradient Descent all make equal use of vectorization.
- Stochastic Gradient Descent
- Mini-Batch Gradient Descent with mini-batch size m/ 2
3. We usually choose a mini-batch size greater than 1 and less than m, because that way we make use of vectorization but not fall into the slower case of batch gradient descent.
- True
- False
4. While using mini-batch gradient descent with a batch size larger than 1 but less than m, the plot of the cost function J looks like this:

You notice that the value of J is not always decreasing. Which of the following is the most likely reason for that? 1 / 1 point
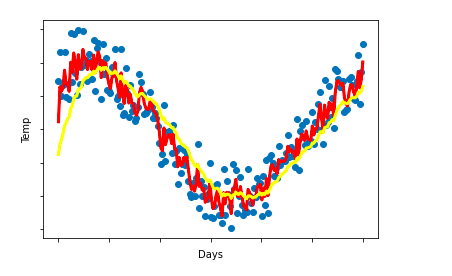
7. You use an exponentially weighted average on the London temperature dataset. You use the following to track the temperature: v t =βv t−1 +(1−β)θ t . The yellow and red lines were computed using values 1 β 1 and 2 β 2 respectively. Which of the following are true?
8. Which of the following are true about gradient descent with momentum?
- Gradient descent with momentum makes use of moving averages.
- Increasing the hyperparameter B smooths out the process of gradient descent
- It decreases the learning rate as the number of epochs increases
- It generates faster learning by reducing the oscillation of the gradient descent process
9. Suppose batch gradient descent in a deep network is taking excessively long to find a value of the parameters that achieves a small value for the cost function ( [ 1 ] , [ 1 ] , . . . , [ ] , [ ] ) J(W [1] ,b [1] ,...,W [L] ,b [L] ). Which of the following techniques could help find parameter values that attain a small value for J? (Check all that apply)
- Try mini-batch gradient descent
- Try turning the learning rate a(alpha)
- Try better random initialization for the weights
- Try initializing all the weights to zero
- Try using Adam
10. Which of the following are true about Adam?
- Adam automatically tunes the hyperparameter a(alpha).
- Adam can only be used with batch gradient descent and not with mini-batch gradient descent.
- Adam combines the advantages of RMSProp and momentum.
- The most important hyperparameter on Adam is € and should be carefully tuned.